O Último Teorema de Fermat

Recentemente o Google homenageou o 410º aniversário de nascimento de Fermat. Há uma história muito interessante sobre esse matemático.

O ano era 1670, a cidade era Toulouse, na França. Clément-Samuel era o filho mais velho do então há 5 anos falecido Pierre de Fermat, cientista e matemático. Desde a morte de seu pai, Clément-Samuel recolhera cartas e anotações e publica o livro Aritmética de Diofante, que continha várias anotações de Fermat. Na página 61 desse livro havia o seguinte teorema:

Não existe nenhum conjunto de inteiros positivos x, y, z e n com n maior que 2 que satisfaz a equação:

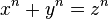
O matemático francês Pierre de Fermat

Repare que, se n for igual a 2, temos o Teorema de Pitágoras, e a igualdade funciona que é uma maravilha. Mas para n maior que 2, não há resultados inteiros positivos que a satisfaçam.

Na margem dessa página, Fermat, que tinha o costume de anotar nas margens dos livros, escreveu:


“Eu tenho uma demonstração realmente maravilhosa para esta proposição, mas esta margem é muito estreita para contê-la.”

O matemático britânico Andrew Wiles

Sendo verdade ou não, por mais de três séculos, praticamente todos os matemáticos, inclusive grandes nomes como Euler e Gauss, tentaram encontrar a tal demonstração mas não conseguiram. Empiricamente, por meio de computadores, se comprova que Fermat tinha razão. Mas a demonstração demorou 358 anos para sair. O matemático inglês Andrew Wiles conseguiu demonstrar o teorema, definitivamente em 1995, mas com conceitos avançadíssimos, com os quais Fermat nem poderia ter sonhado.

O fato é que, ainda hoje, não se tem conhecimento de uma demonstração realmente maravilhosa para o teorema. Será que Fermat usou geometria? Ou indução finita? Ou ainda algo inimaginável? Será que ele quis pregar uma peça na gente? Talvez nunca saberemos...